안녕하세요~! 항상 통계 공부를 하면서 가장 헷갈리는 개념이었는데요,
우리의 선생님인 유튜브를 살펴 보다가 정말 개념을 잘 설명해주신 영상이 있어 공부한 내용을 함께 정리하고자 합니다!
또한, 데이터과학을 위한 통계(2판)의 내용도 함께 참고하였습니다.
출처 : https://www.youtube.com/watch?v=kfl2f8cZwdY&ab_channel=ASDF%EC%98%A4%ED%84%B0%EC%9D%98%ED%86%B5%EA%B3%84
들어가며...
가설 검정 이론에서, 1종 오류와 2종 오류는 각각 귀무가설을 잘못 기각하는 오류와 귀무가설을 잘못 채택하는 오류이다.
출처 : 위키백과
우리는 흔히 통계를 공부하다 보면 흔히 1종 오류와, 2종 오류라는 단어를 접하게 됩니다.
그 때마다 저는 항상 헷갈렸었는데요..
사전적 정의를 살펴봐도 1종 오류는 각각 귀무가설을 잘못 기각하는 오류, 2종 오류는 귀무가설을 잘못 채택하는 오류라고는 하는데...
시험 떄만 열심히 외워서 풀 뿐 그 때 뿐이고, 또 궁금할 떄마다 정의를 찾아 헤매게 되더라구요.
이 글을 읽으시는 분돌 모두가 이번 기회에 정말 1종 오류와 2종 오류의 개념에 대해 저처럼 헤매지 않고
지식을 얻어가셨으면 좋겠습니다 :)
1. 무엇에 대한 오류인가?
1종 오류와 2종 오류에 대해 살펴 보기 앞서 우리는 먼저 단어와 용어의 정의에 대해 생각해 볼 필요가 있습니다.
2가지 오류가 있다는 것은 알겠는데, 오류? 과연 여기서 말하는 오류는 무엇일까요?
바로, 통계적 판단에 대한 오류입니다.
판단 : 증거를 보고 어떤 문장(명제)의 참, 거짓을 결정하는 것
판단은 늘 맞거나 틀리거나 둘중에 하나일 것입니다.
그렇다면 판단과 실제 상황이 맞지 않았을 경우 우리는 통계적 오류가 발생했다고 할 수 있습니다.
우리는 모두 일상에서 어떠한 일에 성공 했을 때는 당연하게 여기는 경향이 있기 때문에
성공 했을 때 얻는 관심에 비해 실패했을 때 더 큰 리스크를 지고, 많은 비난을 받게 됩니다. (지켜보는 사람들도 더 답답하고..)
따라서, 통계적 가설 검정에서도 성공 확률 보다는 실패 확률을 줄이는 것을 목표로 합니다.
그렇다면 통계에서 말하는 실패란 어떤 것들이 있을까요?
2. 제 1종 오류와 제 2종 오류(Type 1 error, Type 2 error)
통계적 유의성을 평가할 때 아래와 같이 2가지 유형의 오류가 발생할 수 있습니다.
1종 오류 : 어떤 효과가 우연히 발생한 것인데, 그것이 사실이라고 잘못 판단하는 경우 [헛다리 짚었다]
2종 오류 : 어떤 효과가 실제로 있는 것인데, 그것이 우연히 발생한 것이라고 잘못 판단하는 경우 [너무 신중해서 답답하다]
교과서 적인 정의는 이렇게 되어 있지만, 저도 늘 정의를 보고 외우기만 할 뿐 사실 기억에는 남지 않는 경우가 너무 많았습니다.
그래서 이번에는 유튜브를 통해 본 예시와, 제가 생각해본 2가지 예시를 통해 1종 오류와 2종 오류의 개념을 살펴보고자 합니다.

(1) 예시
세상 판단을 신중하게 하는 사람과, 무조건 지르고 보는 무지성 난사러가 있다고 가정해보겠습니다.
예시1) 연쇄살인범 찾기 (출처[1])
귀무가설(H0) : 이 사람은 연쇄살인범이 아니다
대립가설(H1, HA) : 이 사람은 연쇄살인범이 맞다
1. 평소 속을 드러내지 않고 조용하다.
2. 때로 멍하게 공상에 잠긴다.
3. 거짓말을 잘하고 간혹 감정이 폭발하여 섬뜩한 느낌을 준다.
4. 재미로 다수 동물을 죽인다.
5. 많은 사람들을 죽인다.
어떤 사람이 연쇄 살인범인지 판단할 때, "조용한 사람은 모두 연쇄살인범이야!"
라고 한다면 세상에 모든 조용한 사람들은(모든 I 분들 모이세요!!) 갑자기 용의선상에 오르는 황당한 상황이 벌어질 것입니다.
그렇다고, 5번 조건이 모두 만족하는 사람만을 용의선상에 올린다면,
그 사이에 더 많은 사람들이 피해가자 되는 안타까운 상황이 벌어질 수도 있을 것입니다.
| 판단(추측) | |||
| 저 사람은 연쇄 살인범이 아니야~ | 저 사람은 연쇄 살인범이 맞아! | ||
| 연쇄 살인범 여부 | X | O | X 경솔/헛다리 [1종 오류] |
| O | X 답답/둔함 [2종 오류] |
O | |
- 1종 오류 : 실제 범인이 아닌데 아무나 붙잡고 범인이라고 하는 경우

- 2종 오류 : 아무리 많은 증거가 나와도 범인이 아니라고 하는 경우

다른 사례를 하나만 더 살펴 보겠습니다!
아래의 예시 2는 위의 영상을 보면서 직접 생각해본 예시입니다.
예시2) 축구에서 공격수가 슈팅 여부를 아래의 기준에 따라 결정한다고 해보겠습니다.
귀무가설(H0) : 이 상황에서는 아무것도 시도하지 않는다(슈팅 X)
대립가설(H1, HA) : 이 상황에서 슈팅을 해야한다
1. 내가 공을 갖고 있다.
2. 수비수를 제치는데 성공했다.
3. 패널티 박스 안으로 들어간다.
4. 슈팅 지점과 골대 중앙의 각도가 30도 이내이다.
5. 골키퍼와 일대일 상황이 된다.
만약 위의 기준에 따라 성향이 극과 극인 2가지 유형의 선수가 있다고 가정해보겠습니다.
(유형 1) 신중러 - 1+2+3+4+5번 기준이 모두 만족되야만 함
공을 잡은 뒤 수비수를 모두 제치고, 패널티 박스 안에서 최적의 각도가 되었을 때, 골키퍼와 일대일 상황이라면 슈팅
(유형 2) 난사러 - 공만 잡으면 무조건 슈팅
1번 기준에 따라 볼만 잡으면 무조건 골대를 향해 슈팅
두가지 유형의 선수(신중러와 난사러) 모두 슈팅을 시도했을 때 득점에 성공할 수도 있고, 실패할 수도 있습니다.
이 때, 2명의 각 선수가 득점에 성공/실패하였을 경우는 2*2 총 4가지 입니다.
4가지 케이스별로 결과를 지켜본 모든 사람들(지도자, 팬, 해설자, 언론 등)은 공통적으로 아래와 같은 반응을 보일 것입니다.
- 비시도+성공가능성 낮았음 : 잘 생각했다. 이런 상황에서는 도전하지 않는게 맞았어
- 시도+실패 : 왜 되지도 않는 상황에서 무리하게 헛다리 짚어..!?
- 비시도+성공가능성 높았음 : 날 새겠다... 이런 것 저런 것 다 따져서 언제 슈팅하게? 왜이렇게 답답해!
- 시도+성공 : 이런 상황에서는 역시 슈팅하는게 맞았어. 결국 골까지 넣었잖아!
| 판단(추측) | |||
| 슈팅 X(비시도) | 슈팅 O(시도) | ||
| 득점 성공 가능성 | X | 1. O | 2. X 경솔/헛다리 [1종 오류] |
| O (100% 가까움) ** |
3. X 답답/둔함 [2종 오류] |
4. O | |
** 위의 예시에서 슈팅을 하지 않았는데, 득점이 된 경우(2종 오류)의 예시는 이론상 불가능한 경우입니다. 그러나 본 예시에서는 같은 상황에서 슈팅을 시도했다면 득점에 성공할 가능성이 거의 100%라고 가정하고, 글을 읽어주시면 감사하겠습니다. (예시를 적다보니까 모순적인 부분이 있네요 ㅜㅜ)
- 1종 오류 : 공만 잡으면 슈팅을 시도하는 선수
- 2종 오류 : 아무리 좋은 찬스가 오더라도 확실하지 않으면 슈팅을 시도하지 않는 경우
3. 어떻게 오류를 줄여야 하나요?
지금까지 1종 오류(헛다리, 난사꾼)와 2종 오류(신중러, 답답이)에 대해 살펴보았습니다.
그렇다면 우리는 어떻게 오류를 줄여야 할까요?
"신중해지세요. 동시에 촉이 좋아지세요"
위의 문장은 누가 보더라도 말이 되지 않습니다. 이처럼 1종 오류와 2종 오류를 모두 줄이는 것은 어렵습니다.
하나를 낮추고 싶게 되면, 나머지 하나는 증가하는 식입니다.(신중해지면 판단이 답답해지고, 판단을 남발하면 정확도는 낮아지겠죠?)
샘플 수를 증가하게 되면 둘 다 모두 낮아지게 되는데, 일반적인 상황에서는 더 많은 샘플 수(데이터 갯수)를 확보하는 것 또한 어렵기 때문에 샘플 숫자가 고정되었을 경우 두가지를 모두 만족시킬수는 없습니다.
마지막으로 통계적 가설 검정에서 자주 나오는 용어들을 살펴 보겠습니다.
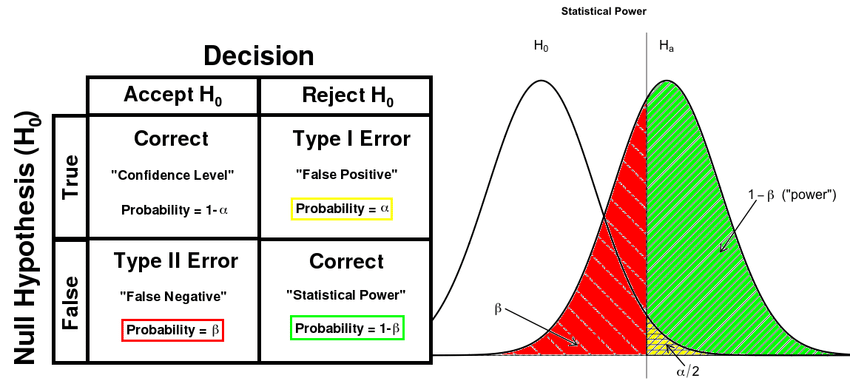
- 유의수준(significance level) : 1종오류가 일어날 확률(α, alpha error)의 최대허용치
- 유의확률(significance probability) 또는 p값(p-value) : 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률 = 결과가 우연해서 비롯했을 확률
- 검정력(statistical power) : 대립가설이 사실일 때, 이를 사실로서 결정할 확률(=
- 검정력이 좋아지면, 2종 오류(β, beta error)를 범할 확률 감소
참고 문헌
[1] 통계 개노답 3형제 (1종 오류, 2종 오류, p값) - 출처 : ASDF 오터의 통계
[2] "데이터 과학을 위한 통계 - 데이터 분석에서 머신러닝까지 파이썬과 R로 살펴보는 50가지 핵심 개념(2판)" |
피터 브루스 , 앤드루 브루스 , 피터 게데크 지음 | 이준용 옮김 | 한빛미디어
[3] Stigler, S. Fisher and the 5% level. CHANCE 21, 12 (2008). https://doi.org/10.1007/s00144-008-0033-3
Fisher and the 5% Level
Published in CHANCE (Vol. 21, No. 4, 2008)
www.tandfonline.com