안녕하세요. 오늘은 정말정말 오랜만에 웹 검색을 하다가 통계에 관한 글을 읽고 내용을 번역하고, 이해한 내용을 정리하고자 글을 남깁니다. 번역이나 문장이 메끄럽지 않더라도 이해 부탁드립니다.
오늘 소개 드릴 글은 'Tivadar Danka'라는 분이 쓰신
"Probabilities, densities, and distributions - Setting common misconceptions straight"
라는 글입니다. 제목에서 보다시피 이 글은 우리가 확률과 밀도, 그리고 분포에 대해서 우리가 잘못생각하고 있는 오해를 바로 세우고자 작성된 글입니다.
저도 읽으면서 헷갈리던 개념을 다시 바로 잡을 수 있었는데요.
그럼 이제 본격적으로 시작해 볼까요?
출처 : https://thepalindrome.substack.com/p/probabilities-densities-and-distributions
Probabilities, densities, and distributions
Raise your hands if you have seen something like this before.
thepalindrome.substack.com
이 글은 다음과 같은 목차로 이루어져 있습니다.
확률
확률 변수
확률 분포함수
확률 밀도함수
정규분포
결론

혹시 여러분은 위의 수식이 뭔지 알고 계신가요? 이 수식은 표준 정규 분포(standard normal distribution)을 나타내는 수식입니다.
그리고, 우리는 종종 이를 "확률(probabilirty)"이라고 말하곤 하죠.
하지만 우리가 얼핏 생각하기엔 전혀 이상할 게 없어보이지만 이 수식은 확률이 아닙니다.
그렇다면 확률은 무엇인가요?
확률 (probability)
확률은 집합으로 표현되는 사건(이벤트)을 입력하면 확률값(0과 1 사이의 실수)을 반환하는 함수 P(A)입니다.
함수 P는 확률 측정(probability measure)이라고도 합니다.
이벤트는 소위 표본 공간(sample space)의 하위 집합으로, 그리스어 오메가 Ω로도 표시 되는 집합입니다.

확률은 일반적으로 처음 이를 주장한 러시아 수학자인 콜모고로프의 이름을 따서
콜모그로프의 공리(Kolmogorov’s axioms)를 만족하는데.
3가지 조건은 음이 아님(nonnegativity), 전체 표본 공간의 확률의 합계는 반드시 1(the probability of the entire sample space must be 1), 가산성(additivity) 입니다.

하지만, 우리가 확률을 직접 다루는 것은 어렵기 때문에 대부분 확률 변수(random varibles)를 통해 확률 및 이벤트와 상호 작용합니다.
확률 변수(Random Variables)
우리가 사는 세상은 온통 확실하지 않은 것들 뿐입니다.
내일 비가 올지, 출근길에 버스가 몇분뒤에 도착할지(안내시스템을 볼 수 없다는 가정하에), 복권에 당첨될 수 있을지 없을지 등 온통 확실하지 않은 것들 투성이입니다.
우리는 이러한 불확실성(uncertainty)을 조금이나마 극복하기 위해 세상에서 벌어지는 일들을 관찰하고, 기록하게 되었습니다.
예를 들어 전구의 수명을 알고 싶을 때 생산 라인에서 나오는 모~~든 전구를 망가질 때 까지 켰다가 작동되지 않는 시간을 측정할 수 도 있겠지만 그렇다면 시장에 내놓을 수 있는 전구가 하나도 남지 않게 되겠죠?
따라서 전구 중 일부만을 표본으로 추출하여 수명을 측정하게 될 텐데, 이 상황에서는 '전구 수명을 측정한 측정값'이 확률 변수가 되고
이는 확률 이론의 주요 대상 중 하나입니다.

또한, 수학적으로 확률 변수는 표본 공간(Ω)를 실수 집합에 매핑하는 함수입니다.
이 개념을 이해하기 위해서는 다음 그림을 보면 됩니다.

이런 정의에는 심각한 문제가 있는데요.
표본 공간과 확률 변수는 실제로 쉽게 사용하기에는 너무 추상적입니다.
예를 들어, "전구의 수명"은 정확한 수학 공식으로 표현할 수 없기 때문에 정량적인 분석을 수행할 수 없습니다.
그렇다면 이 문제를 해결하기 위한 방법은 없을까요?
우리는 확률 변수 X를 사용해 표본공간(Ω)에서 실수 집합으로 확률 측정 P를 매핑합니다.
(확률) 분포 함수 (Distribution Functions)
대부분의 경우 우리는 X가 주어진 범위에 속할 확률과 같은 질문에 관심이 있습니다. 예를 들어 "이 전구가 1년 안에 망가질까?"와 같은 질문입니다.
결과적으로 이러한 확률을 아는 것이 확률 변수(random variable)를 이해하는 데 필요한 전부입니다.
수학적으로 정확하게 말하자면, 우리는 소위 레벨 세트를 보고 있습니다.
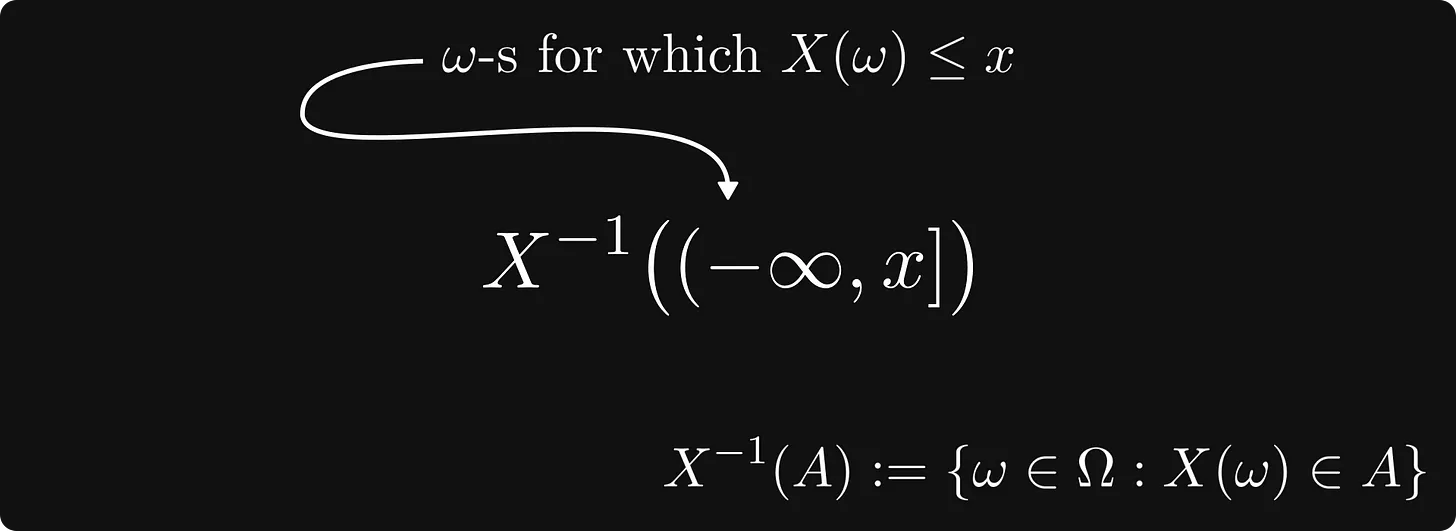
위의 그림은 이해하기는 커녕 보자마자 머리가 아파오는 것 같습니다. 그래서 바로 아래 그림과 같이 시각화 할 수 있습니다.
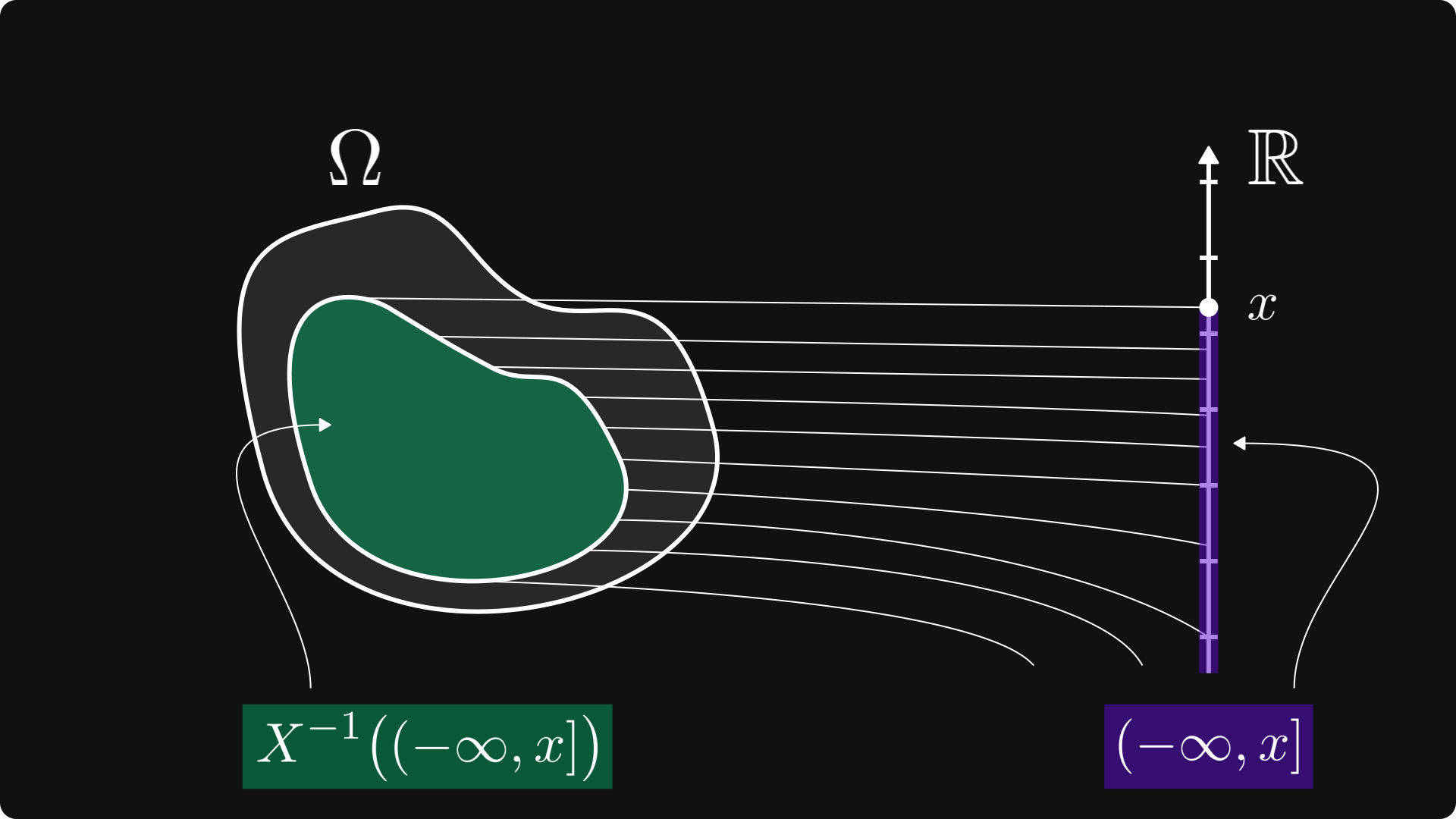
레벨 셋의 요소는 X에 의해 범위 (-∞, x]에 매핑됩니다.
레벨 셋의 확률은 확률 변수에 대한 모든 관련 정보를 인코딩합니다.
x를 변수로 본다면 이러한 수량을 사용하여 실제 함수를 정의할 수 있습니다.
즉, 실제 확률 변수 대신(proxy) 사용할 수 있는 것입니다.
이 함수를 누적분포함수(또는 간단히 CDF)라고 하며 확률 이론과 통계의 초석입니다.
다음은 정확한 정의입니다.
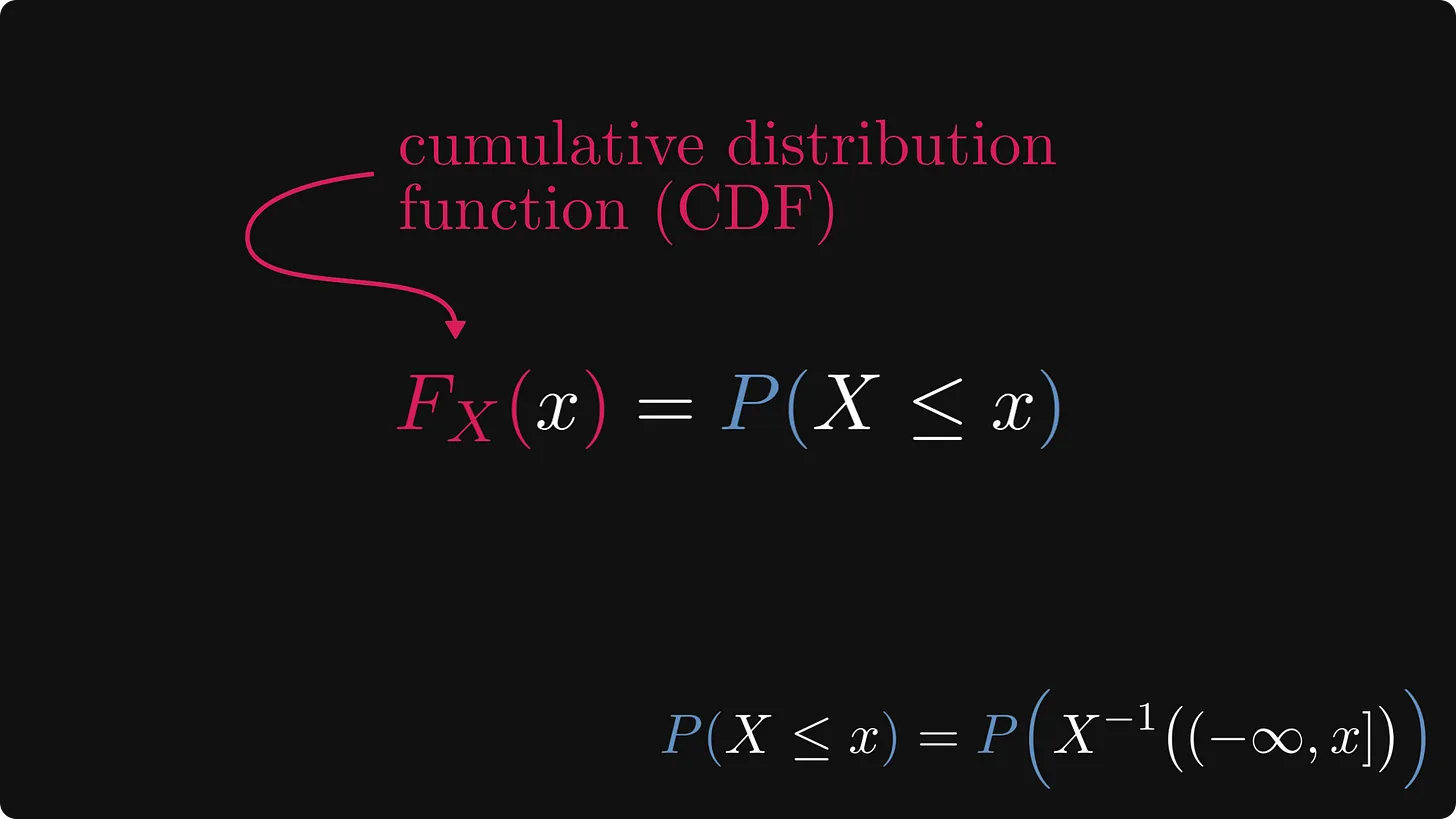
확률 측정 수식의 인수 내부에 있는 “X ≤ x“ 는 레벨 셋의 약어고, 훨씬 간결하기 때문에 일반적으로 이 방법이 주로 사용됩니다.
예를 들어 전구의 수명은 다음 수식과 그림과 같이 지수적으로 분포한다고 정의됩니다,
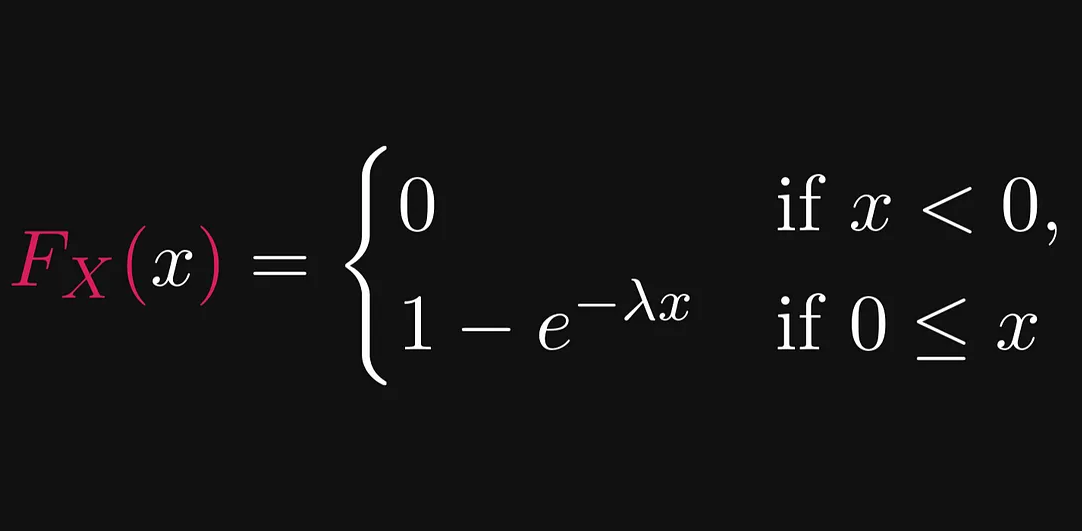
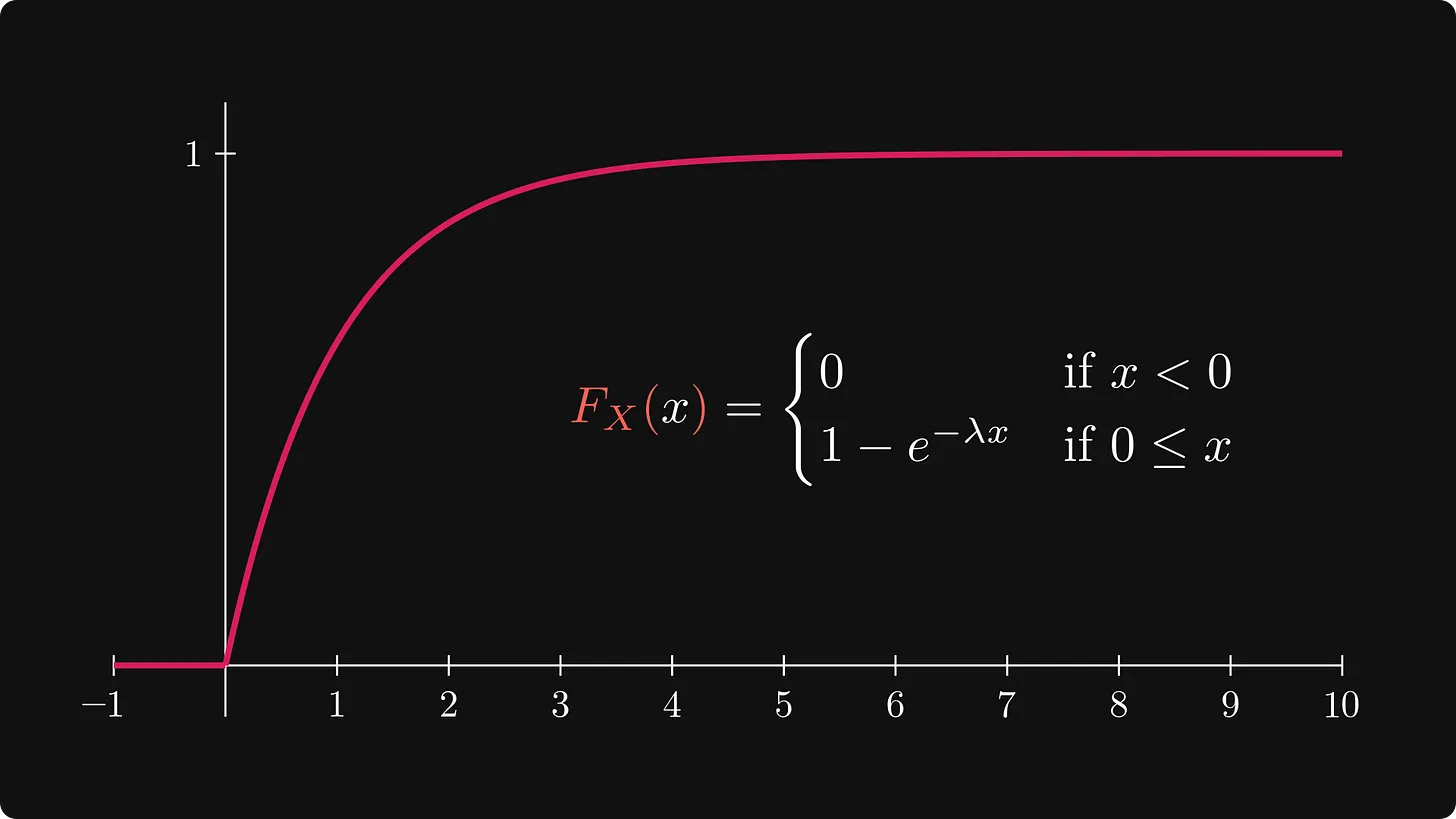
위의 그림 중 왼쪽 그림을 보면 지수 분포 함수에서 λ(람다) 문자가 있는데 이는 분포의 모양을 결정하는 매개변수(parameter)라고 생각하면 됩니다.
지수 분포 함수는 우측 그림과 같이 x가 커질수록 누적 분포 합이 지수적으로 증가하는 모양을 보입니다.
세상에는 수 많은 확률 분포가 있습니다. (예를 들면, uniform, Gaussian, Pareto, Weibull, Cauchy 등등)
그러나 누적 분포 함수에는 중요한 단점이 있습니다. 기본적으로 전역 정보(global information)만 전달하고, 지역 정보(local information)을 전달하지 못한다는 것입니다.
지역 정보란 범위가 아니라 내가 관심있는 특정 지점 (예> x = 1.4)에 관련한 정보를 의미하는 것 같습니다.
(확률) 밀도 함수 (Density Functions)
우리의 확률 변수 X에 대해 한 번 더 이야기해 봅시다. X가 우리 전구의 수명이라는 것을 기억하세요.
x초 후 정확히 전구가 꺼질 확률은 얼마인가요? 즉, 우리는 P(X = x)의 수량을 찾고 있습니다.
간단한 계산을 해보면 실제로는 0이라는 것을 알 수 있는데, 이것은 꽤 놀라운 일입니다.
극한의 정의에 따라 아래 수식에서 입실론 값이 매우 작은 값이라고 한다면, 두번째 줄에서 왼쪽 항의 값과 오른쪽 항의 차이가 매우 작아져 0에 수렴하게 됩니다.
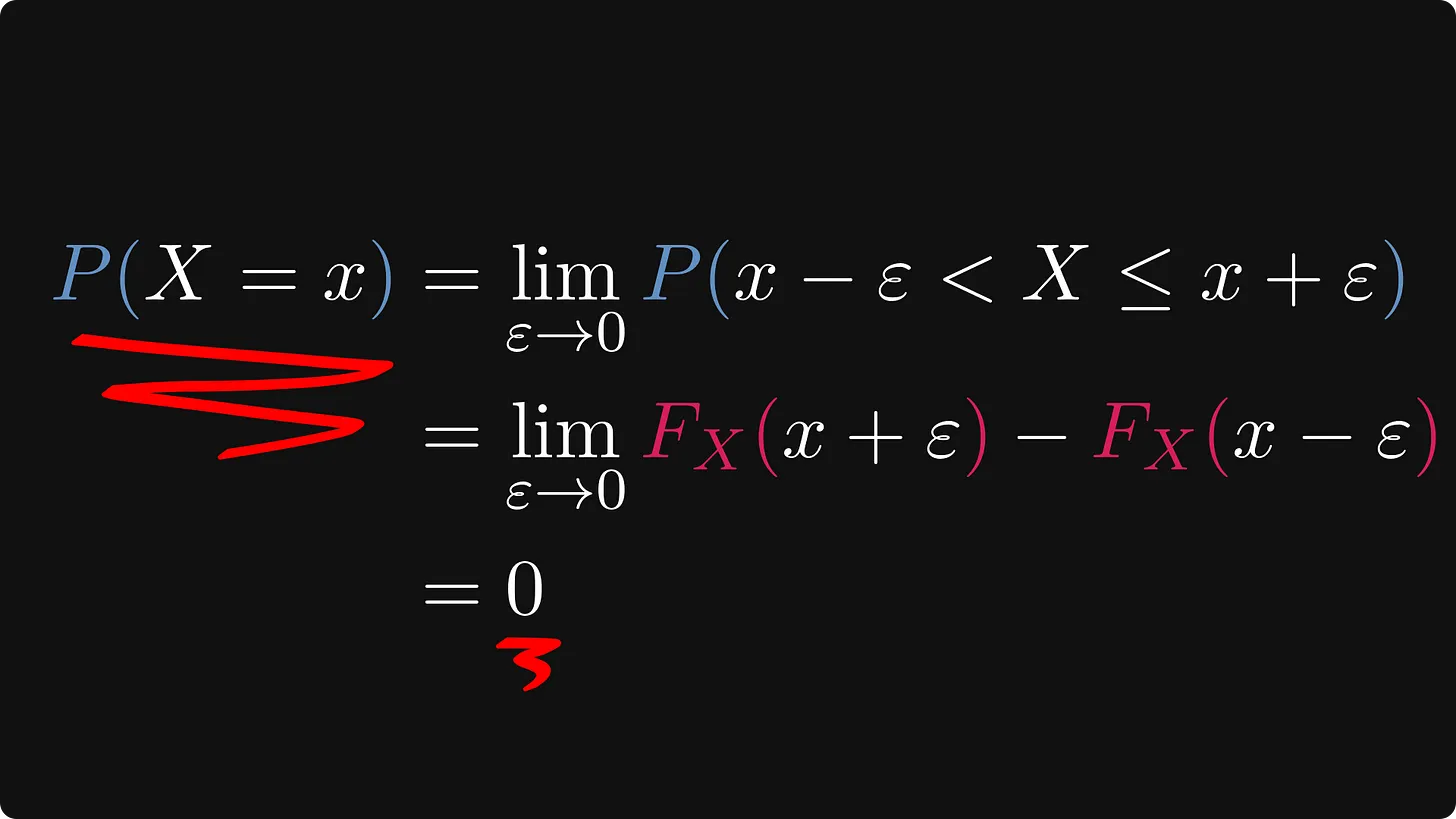
즉, 각 결과의 확률은 예외 없이 0입니다. 그러나 기하급수적으로 분포된 X는 지루함과는 거리가 멉니다. (오히려 반대입니다)
이것은 지수 분포에만 해당되는 것은 아닙니다. 이것은 유니폼, 가우스, 파레토, 그리고 다른 많은 것들에서도 마찬가지입니다.
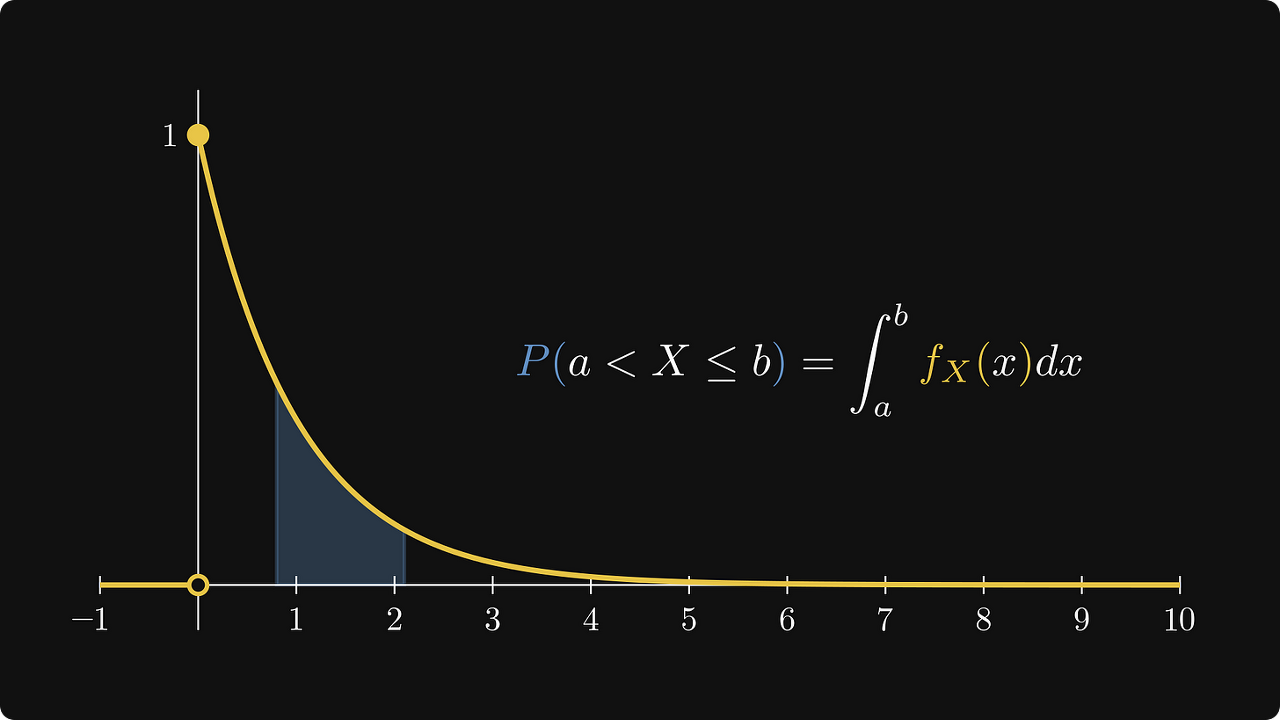
이상하지 않나요? 우리는 간단히 CDF의 증분에 따라 X가 세그먼트(a, b) 사이에 떨어질 확률을 값으로 표현할 수 있습니다.
아래 공식을 참조하십시오:
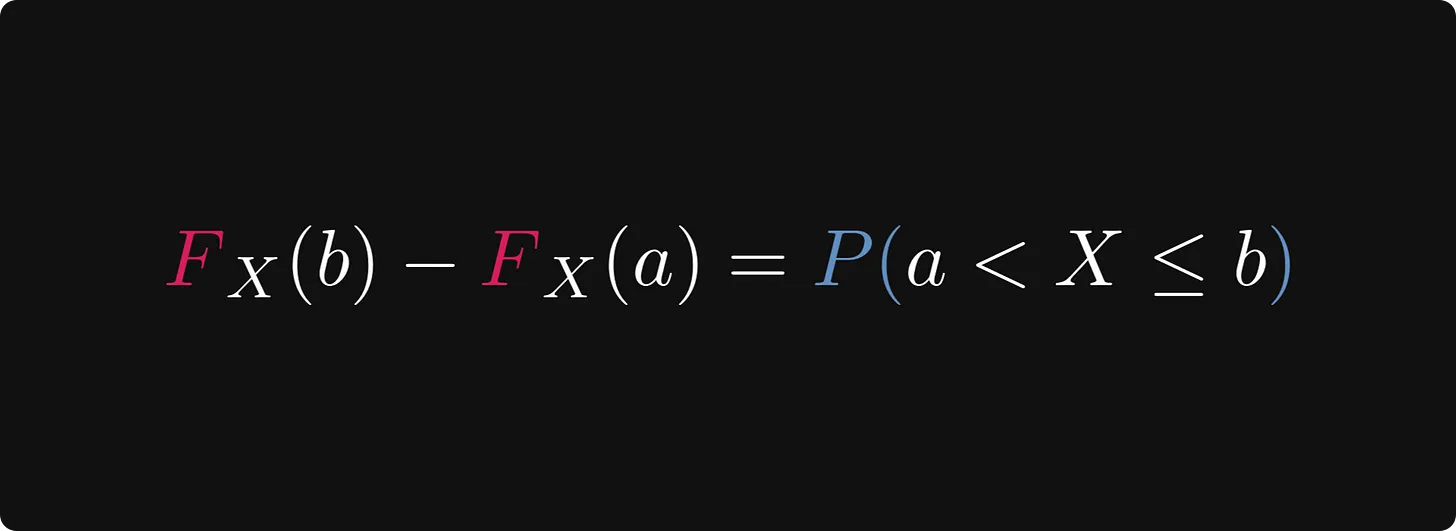
왼쪽의 CDF 증분, 오른쪽의 세그먼트 (a, b]에 X가 떨어질 확률.
이것이 친숙해 보입니까? 자세히 살펴보면 이 공식은 미적분학의 기본 정리와 매우 유사합니다.
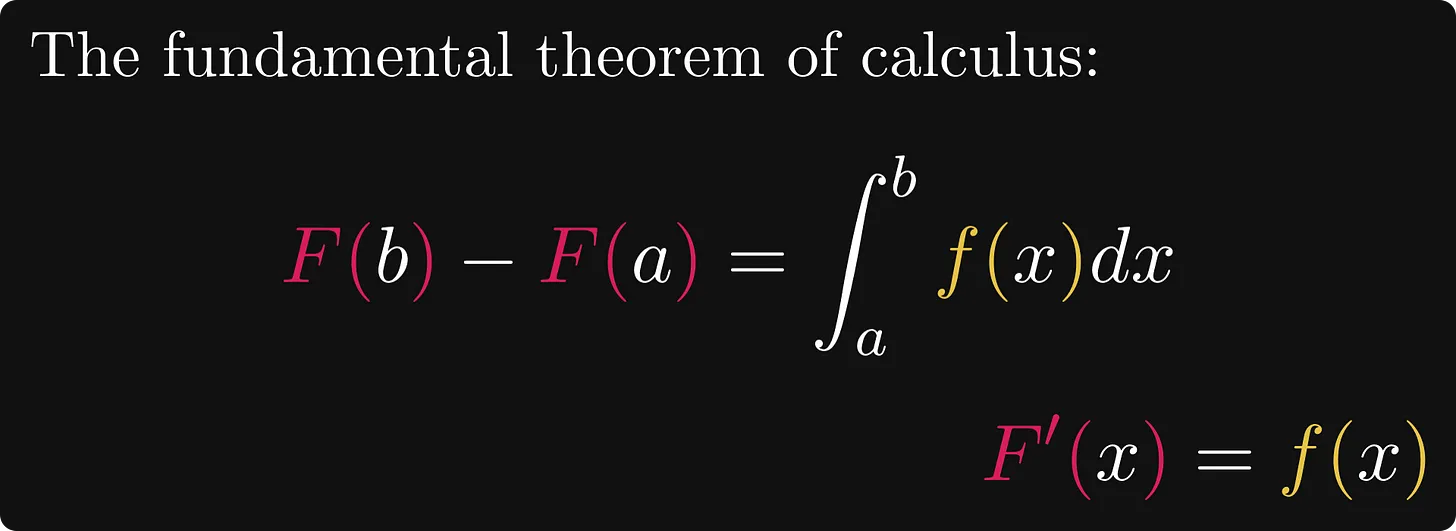
수식에서 왼쪽(F(b)-F(a))은 함수 F의 증분, 오른쪽(f(x)에 대한 a에서 b 구간의 적분값)은 미분의 적분.
따라서 오른쪽 함수는 통합을 통한 분포 함수를 나타내고, 확률 변수에 대한 로컬 정보를 전달합니다.
정확히 우리가 원했던 것입니다!
이 함수는 매우 특별해서 고유한 이름을 가지고 있습니다. 즉, 확률 변수 X의 확률 밀도 함수(또는 줄여서 PDF)입니다.
정확한 정의는 이렇습니다. 구간 [a, b]에 대한 적분 값과 누적 분포 함수의 증분이 같은 함수가 존재하는 경우 X의 밀도 함수라고 합니다.

만약, CDF 가 미분 가능하다면, 이것의 미분은 분포 함수(density function)이 되는 것입니다.
if the CDF is differentiable, its derivative is a density function
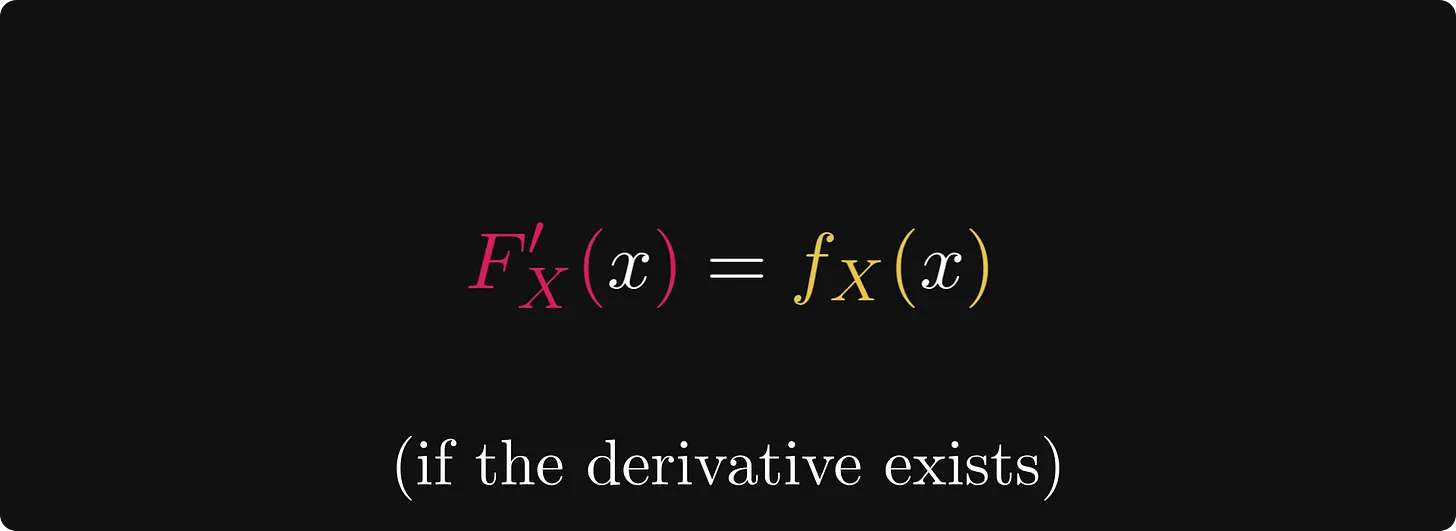
이전 문장에서 "the" 대신 관사 "a"를 사용한 것을 유심히 봐주세요. 이는 밀도 함수가 고유하지 않기 때문입니다.
그것에 대해 생각해보십시오. 단일 지점에서 값을 수정하면 적분은 변경되지 않습니다.
밀도 함수가 존재하기 위해 CDF의 모든 미분 가능성이 필요하지 않다는 점에 주목해야 합니다.
그 중 하나가 반복되는 예인 지수 분포의 밀도 함수가 있습니다.
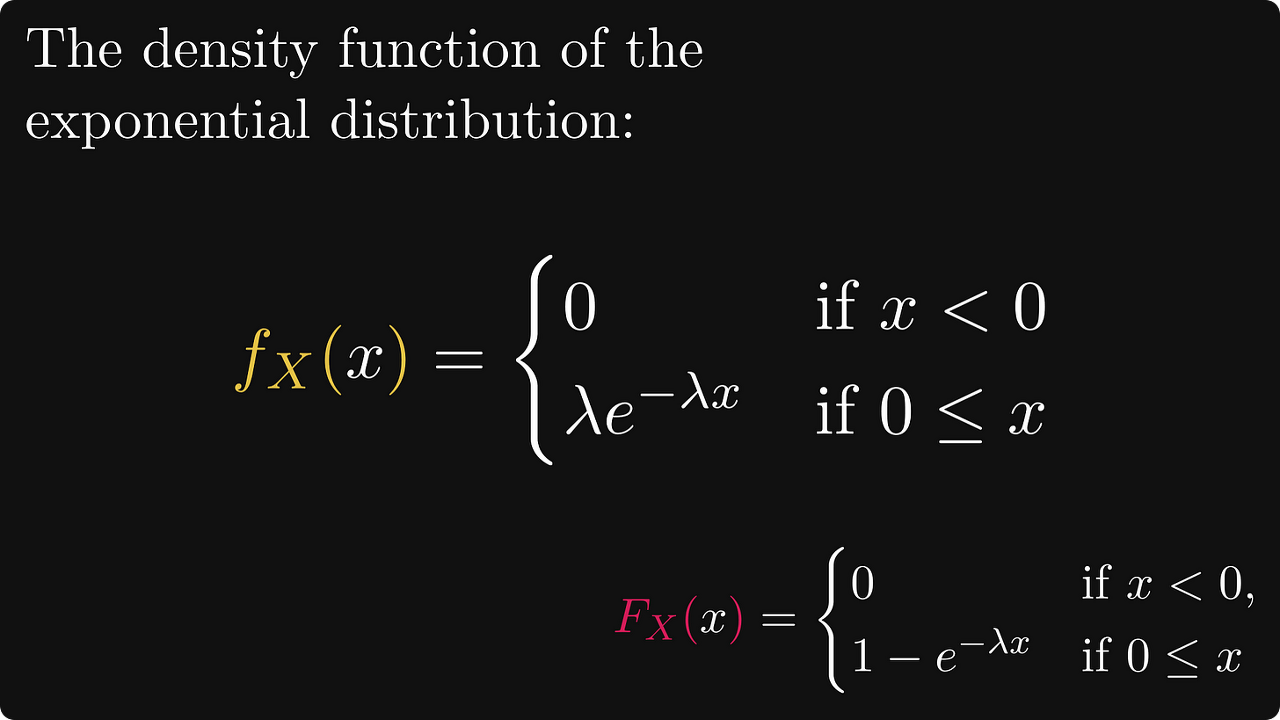
다시 말하지만, 지수 CDF는 0에서 미분 가능하지 않지만 다른 곳에서는 미분 가능하며 거기에서 도함수는 PDF를 제공합니다.
이것이 플롯에서 보이는 방식입니다.
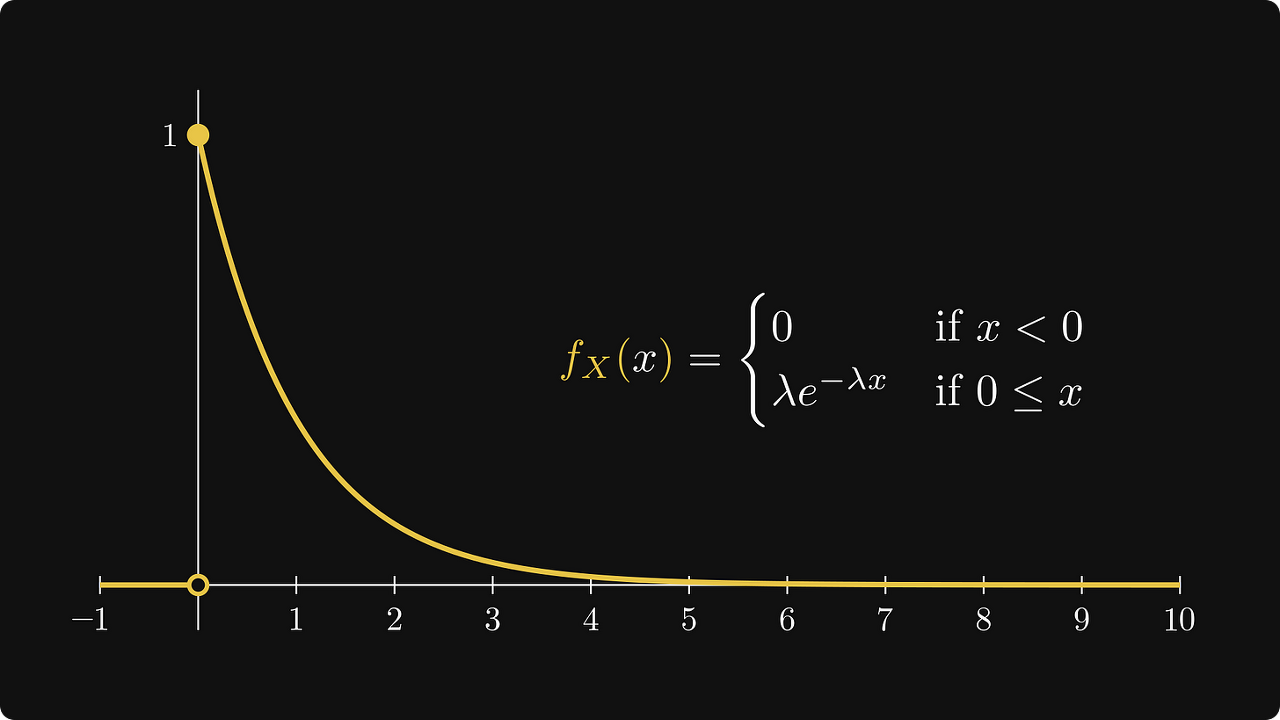
밀도를 확률 분포의 "지형 지도"로 상상할 수 있습니다.
개별 결과의 확률이 0이더라도 밀도 함수는 x가 커질수록 확률이 점점 더 낮아진다는 것을 명확하게 보여줍니다.
적분 값이 곡선 아래 영역에 해당하므로 확률에 대한 새로운 해석을 제공합니다.
정규 분포(The normal distribution)
시작 예제인 종 모양 곡선(벨 커브)를 다시 살펴보겠습니다. 이것은 표준 정규(또는 가우시안) 분포의 밀도로 알려져 있습니다.

표준 정규분포의 밀도는 0 근처에 집중되고 우리가 0 에서 멀어지면 낮아집니다.
한 가지는 확실합니다. 확실히 확률이 아닙니다.
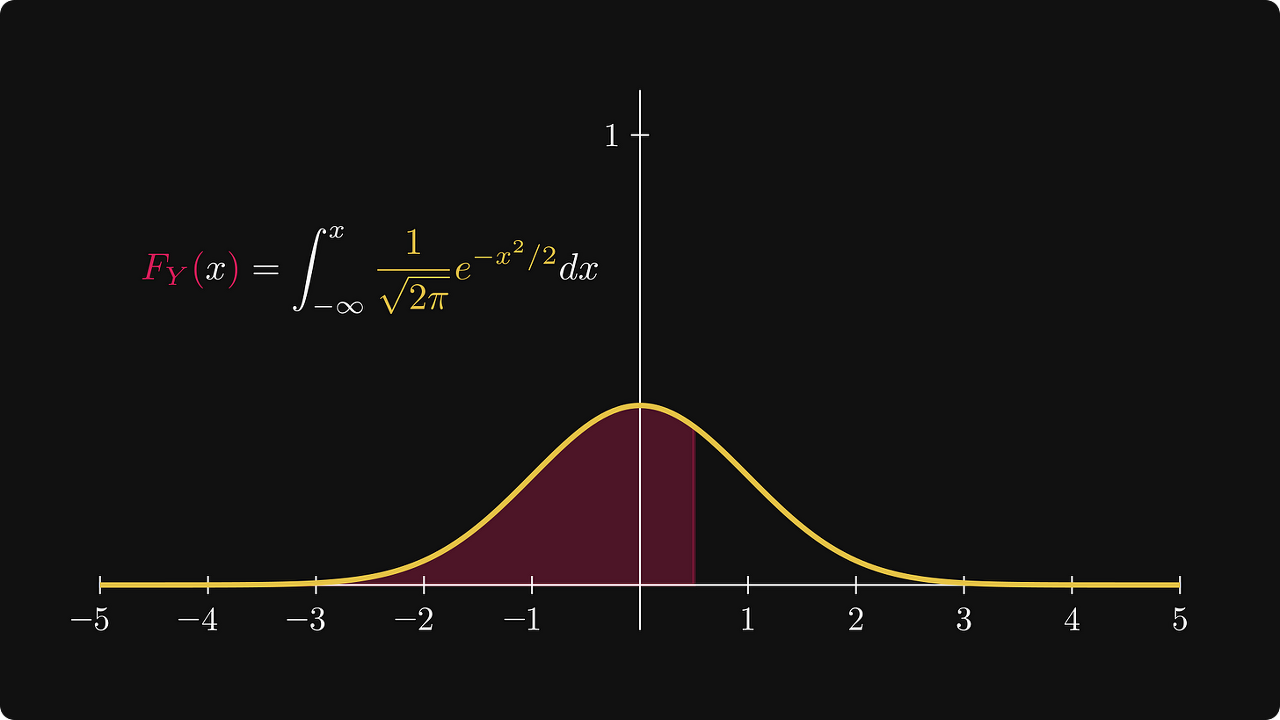
이 경우 밀도 함수가 훨씬 더 중요합니다. 왜요? 정규분포의 누적분포함수는 닫힌 형태(closed form)로 표현할 수 없고 적분으로만 표현하기 때문입니다.

닫힌 형태로 표현할 수 없다는 것은 수학자들이 그렇게 할 만큼 똑똑하지 않다는 것이 아닙니다.
그러한 공식은 세상에 존재하지 않으며 우리는 이것을 증명할 수 있습니다. (저자는 이것에 대해 저자를 믿어야 한다고 했습니다. 그것은 현재 게시물의 범위를 훨씬 넘어선다고 합니다.)
결론(Conclustion)
지금까지 배운 내용을 정리해 봅시다.
확률 변수는 확률 이론과 통계의 중심 대상이지만 직접 다루기는 매우 어렵습니다. 그 이유는 두 가지입니다.
- 샘플 공간 Ω은 매우 추상적일 수 있습니다.
- 확률 변수는 종종 다루기 쉬운 공식이 없고 "전구의 수명", "사람의 무게" 또는 이와 유사한 것과 같은 모호한 설명만 있습니다.
이러한 모호함을 해결하기 위해 추상 상태 공간에서 실수 집합으로 무작위 변수를 전송하는 도구인 누적 분포 함수를 도입했습니다.
분포 함수는 임의의 실수에서 임의 변수의 동작에 대한 로컬 정보를 전달하지 않기 때문에 충분하지 않습니다.
그러나 그들의 파생물은 확률 밀도 함수의 개념으로 이어집니다. 이들은 종종 확률과 혼동되지만 그렇지 않습니다.
오히려 분포의 변화율을 설명하여 "지형 지도"를 제공합니다.