안녕하세요!
오늘도 링크드인을 보다 다시 한번 복습하기 좋은 글이 있어서 정리하여 공유드립니다. 작게나마 도움이 되었으면 좋겠습니다!
주성분 분석과 선형 판별 분석은 차원 축소할 때마다 가장 먼저 떠오르는 용어들입니다.
하지만, 각각이 무엇인지 배우고 듣지만 계속 까먹게 되더라구요. 그래서 먼저 요즘 핫한 ChatGPT에 질문해 보았습니다.

내용을 요약하자면,
주성분 분석(Principal Component Analysis)
차원 축소를 위해 데이터 분석과 머신러닝 분야서 쓰이는 기법으로, 비지도 방법(데이터에 클래스 레이블이 주어지지 않은 경우)입니다.
PCA는 데이터에서 가장 큰 분산(변동)을 설명하는 주성분(Principal Component)이라고 하는 선형적으로 상관관계가 없는 새로운 변수 세트를 찾는 방식으로 작동합니다.
새로운 변수는 원래 데이터를 더 낮은 차원의 데이터로 표현하는데 쓸 수 있으며, 이는 시각화에 유용하고 일부 기계 학습 알고리즘의 계산에 필요한 자원을 줄이는 데 유용할 수 있습니다.
선형 판별 분석(Linear Discriminant Analysis)
차원 감소를 위해 데이터 과학에서 사용되는 또 다른 기술로, 지도 방법(클래스 레이블을 사용)입니다.
LDA는 데이터의 서로 다른 클래스 간의 분리를 최대화하는 피쳐(변수)의 부분 공간(subspace, 전체 공간의 일부) 공간을 찾는 것을 목표로 합니다.
이는 기능 공간에서 서로 다른 클래스를 분리하는 데 도움이 되므로 분류 작업에 유용할 수 있습니다. LDA는 데이터가 정규분포를 따르고, 다른 클래스들의 공분산 행렬이 일치하다는 가정을 기반으로 합니다. 이러한 가정은 LDA를 사용할 때 고려해야 할 중요한 사항입니다.
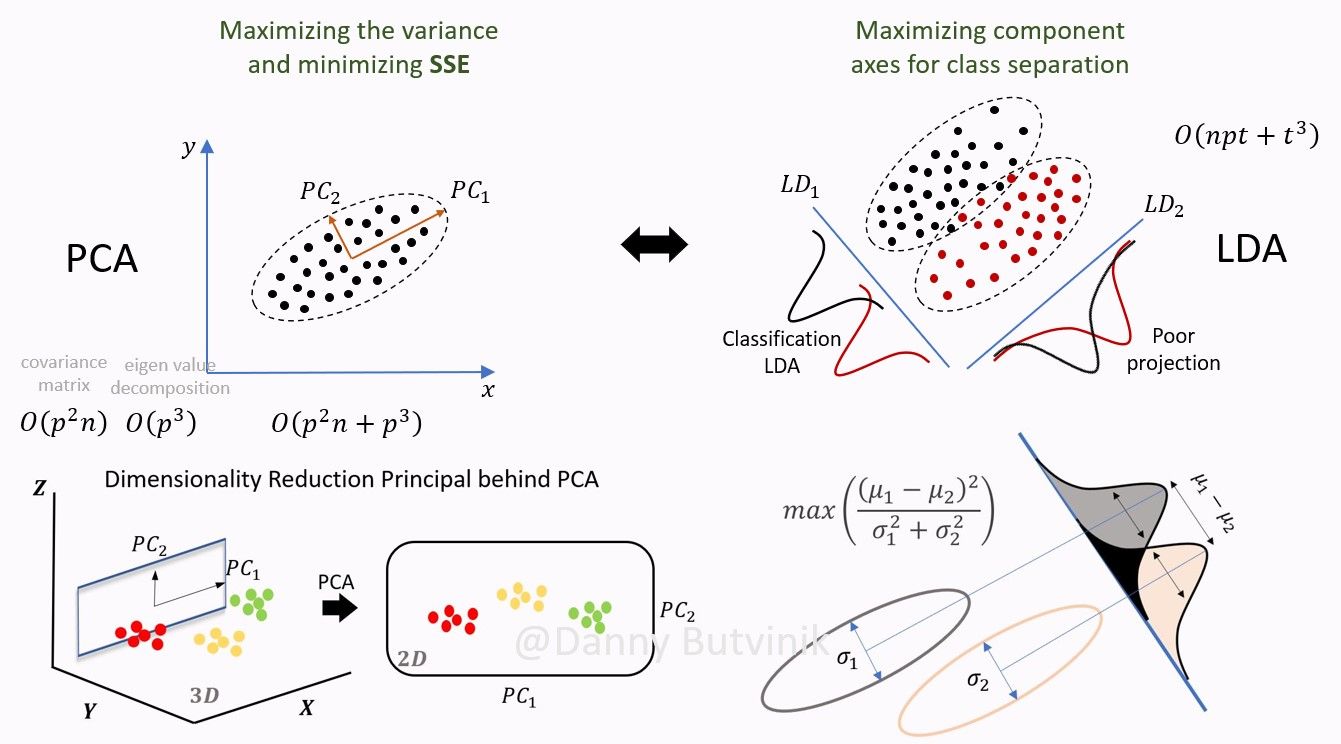
말로만 보면 헷갈릴 수도 있으니 다시 위의 그림을 보며 정리해보았습니다.
| PCA | LDA |
| 분산을 최대화 하는 방향 찾기 | 클래스 간 분리가 가장 잘 이루어 질 수 있는 피쳐의 부분 공간 찾기 |
| 비지도학습 | 지도학습 |
| 클래스당 샘플 수가 적은 경우 성능 우수 | 다중 클래스를 가진 큰 데이터 셋에서 성능 우수 차원 축소시 클래스 구분성이 중요 |
| 등분산성, 정규성 등 모수적 가정을 만족해야함 |
LinkedIn Danny Butvinik 페이지: #machinelearning #datascience | 댓글 11
In Data Science and Machine Learning, PCA is an unsupervised dimensionality reduction technique that ignores the class label. PCA focuses on capturing the… | 댓글 11
www.linkedin.com
예시 코드
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import pandas as pd
# Scale the train set : PCA 수행 전 반드시 데이터 스케일링을 해주어야 함
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
# Perform PCA on the scaled train set : 전체 변동 중 95%의 변동을 설명할 수 있는 갯수 만큼 주성분 도출
pca = PCA(n_components=0.95)
X_train_pca = pca.fit_transform(X_train)
# Apply the same transformation to the test set : 테스트 셋에도 동일한 변환 수행
X_test = scaler.transform(X_test)
X_test_pca = pca.transform(X_test)
# Determine explained variance using explained_variance_ration_ attribute : 설명 가능한 분산 비율 확인
exp_var_pca = pca.explained_variance_ratio_
# Cumulative sum of eigenvalues; This will be used to create step plot for visualizing the variance explained by each principal component.
cum_sum_eigenvalues = np.cumsum(exp_var_pca)
# Create the visualization plot
plt.bar(range(0,len(exp_var_pca)), exp_var_pca, alpha=0.5, align='center', label='Individual explained variance')
plt.step(range(0,len(cum_sum_eigenvalues)), cum_sum_eigenvalues, where='mid',label='Cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
# PCA 결과 생성된 데이터셋(X_train_pca)의 컬럼명을 PC1, PC2, ... 식으로 이름 붙이고 데이터프레임에 저장
pc_cols = ['PC{}'.format(i+1) for i in range(X_train_pca.shape[1])]
tmp_pca_df = pd.DataFrame(X_train_pca, columns = pc_cols)
출처 : https://vitalflux.com/pca-explained-variance-concept-python-example/
PCA Explained Variance Concepts with Python Example - Data Analytics
Data Science, Machine Learning, Data Analytics, Python, R, Tutorials, Interviews, AI, PCA, explained variance, concepts, examples, real-world
vitalflux.com
'Data Analysis' 카테고리의 다른 글
| [번역] 당신은 Train, Validation & Test Set을 올바르게 사용하고 있습니까? (0) | 2023.11.28 |
|---|---|
| Over Sampling for Regression (0) | 2023.11.01 |
| [Python] Lambda 함수 사용법(for 데이터분석가) (2) | 2023.03.15 |
| 분류 문제의 평가지표 (PRECISION, RECALL, ACCURACY 등) (0) | 2022.04.12 |
| [Python] iris dataset load & pre-processing (0) | 2022.02.10 |



